七桥问题一笔画图解怎么走顺序
七桥问题一笔画图解怎么走顺序 大数学家欧拉把它转化成一个几个问题一笔画问题。上图中的七条线代表七座桥,红点代表它们相交的点。欧拉发现只有当笔沿着一条弧线到达交点后,又能沿着另一条弧线离开,也就是交汇于这些点的弧线成双成对时,一笔画才能完成,这样的交点就称为“偶点”。七桥问题一笔画答案
1、七桥问题其实是个网红数学题:18世纪普鲁士哥尼斯堡(现俄罗斯加里宁格勒)有七座桥连接两个小岛和河岸,当地人纠结:能不能不重复、一次走完所有桥? 这题当时火到连欧拉都知道了。
2、欧拉的操作很秀:他没用脚丈量,而是把陆地简化成点、桥变成线,硬生生把实际问题抽象成了“一笔画”几何问题——这才发现关键不是桥多桥少,而是路径的奇偶点数量。
3、破解全靠“奇点”数:欧拉总结出规律:一个图形能一笔画成,必须满足奇点(连接线条数为奇数的点)数量是0或2,但七桥模型对应四个点全是奇点(每个点连着3或5条线),彻底没戏!
4、结论直接封神:欧拉1736年宣布“七桥无法一次不重复走完”,顺便开创了图论这个数学分支,现在你手机导航的路径规划,底层逻辑都有这个理论的影子。

5、现代人别试了:虽然原桥二战后被毁,但即使重建也走不通——数学定律吊打体力,不过换个思路:如果拆掉一座桥(减少两个奇点),就能一秒变可行啦!
相关问题解答
1、七桥问题到底是啥?
简单说就是18世纪哥尼斯堡(现在叫加里宁格勒)有七座桥,连接着两条河和两个小岛,当地人好奇:能不能不重复、不遗漏地一次走完所有桥?最后数学家欧拉证明这事儿根本不可能——所以没有“正确走法”,因为压根儿走不通!
2、为啥一笔画不走通七座桥?
欧拉发现,这问题关键看“奇点”(连接奇数条线的点)的数量,如果奇点超过2个,就不可能一笔画成,七桥问题里有4个奇点(两个岛和两岸),所以绝对没法一次走完还不重复。
3、那有没有类似能一笔画的问题?
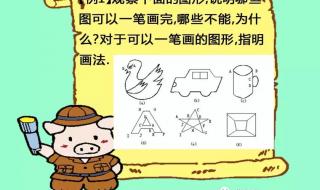
有啊!比如正方形加两条对角线,或者“日”字格——只要奇点数是0或2就能一笔画,比如从其中一个奇点出发,另一个结束,就能搞定。
4、欧拉咋解决这问题的?有啥意义?
欧拉直接把地图抽象成点和线,用数学证明了不可能,还开创了“图论”这个数学分支,现在地铁规划、网络路由啥的都用得上——所以别纠结咋走了,人家答案就是“不可能”!
本文来自作者[冷月无声]投稿,不代表迅优号立场,如若转载,请注明出处:https://www.octobercms.cn/wiki/202510-8.html



评论列表(3条)
我是迅优号的签约作者“冷月无声”
本文概览:七桥问题一笔画图解怎么走顺序七桥问题一笔画图解怎么走顺序 大数学家欧拉把它转化成一个几个问题一笔画问题。上图中的七条线代表七座桥,红点代表它们相交的点。欧拉发现只有当笔沿着一条...
文章不错《七桥问题一笔画图解怎么走顺序 七桥问题一笔画答案》内容很有帮助